Arte y dimensiones extra

Imagínate que quieres concertar una cita con un amigo en un centro comercial. Para que los dos os encontréis será necesario que le proporciones una serie de información, concretamente, la hora de encuentro, la planta y el cruce de pasillos específico. Es decir, tres datos espaciales y un dato temporal, cualquier otra información que le proporciones, es redundante en cuanto al objetivo de la comunicación. Esta es la consecuencia de vivir en un universo con 3 dimensiones espaciales y 1 dimensión temporal, ¿o no es así nuestro universo?

Durante muchos años, los autores de ciencia ficción han ideado y especulado sobre dimensiones extra que nos permitan escapar de las rejas de nuestro mundo tridimensional (tetradimensional al considerar el tiempo). Incluso videntes y chamanes han afirmado en diferentes culturas su capacidad de viajar a otras dimensiones. Lo que se podría equiparar a día de hoy con las decenas de conspiranoicos que se aglomeran en las redes sociales para difundir mensajes de lo más excéntricos, entre los que destaca la idea de la existencia de otras dimensiones a las que solo unos pocos privilegiados (como los reptilianos) tienen acceso. Sin embargo, desde hace tiempo que la comunidad física ha introducido los supuestos de dimensiones extra, para poder explicar de una forma efectiva diversos modelos de la teoría unificada, como la afamada teoría de cuerdas o su extensión, la teoría M. Pero, ¿cómo podemos concebir más dimensiones de las que podemos percibir con nuestro sentidos?

"Relatividad" litografía de Maurits C. Escher

Por ejemplo, para entender una cuarta dimensión, te puedes centrar en un salto inferior, el de 2 a 3 dimensiones. Imagina que tienes una pelota en una mesa encerrada por una cuerda circular, si quieres extraer la pelota del círculo, sin separarla de la mesa (en 2 dimensiones) la tarea resulta imposible. Sin embargo, si introduces la pelota en la 3 dimensión (la altura en este caso) la tarea te resultará de lo más sencilla. Aun así estas preguntas son enigmas muy actuales, basados en las necesidades de dimensiones extra de las teorías modernas de la física. Muy pocos pensadores previos reflexionaron acerca de otras dimensiones que fueran las que les mostraban sus ojos. Pero en el siglo XVIII si hubo uno, el gigante intelectual de Koenigsberg, Immanuel Kant. En su primera etapa, el reputado filósofo, estaba más interesado por la ciencia que por la filosofía, y mientras estudiaba los trabajos de Newton, atendiendo a su ley de la gravedad, determinó que el cuadrado de la distancia propuesto en esta fórmula, estaba íntimamente ligado al espacio en 3 dimensiones. Si el espacio tuviese cuatro, la distancia en la fórmula estaría elevada al cubo, si tuviese 5 dimensiones, estaría elevada a la 4 potencia. Es decir, en un mundo de N dimensiones, las fuerzas de atracción gravitatorias decaerían con la (N-1)ésima potencia de la distancia que separa los dos cuerpos. Debido a estas causas, Kant supuso que el universo debería tener 3 dimensiones para así poder explicar la ley de gravitación universal de Newton. Sin embargo, la situación es la inversa, es la tridimensionalidad del espacio la que permitió a Newton realizar las observaciones necesarias para explicar su ley de gravitación.

Atender a aquellos mundos o universos que muestran un número mayor o menor de dimensiones es una tarea cognitivamente compleja, pero resulta más sencilla en el caso de suponer menos dimensiones que las que percibimos. Por ejemplo, en el caso en el que viviéramos en un mundo de 2 dimensiones, si realizaremos caminatas en direcciones aleatorias, al final regresaríamos al punto de partida; mientras que en el mundo tridimensional que habitamos las caminatas aleatorias no nos permitirían llegar nunca al punto de partida original, ¡Nos podemos perder gracias a la tercera dimensión! Es decir, pasar de un número de dimensiones a otro mayor, aumenta la complejidad del mundo observado, ¿o no siempre ocurre así? Lo cierto es que no. En ocasiones, los mundos con más dimensiones se vuelven más restrictivos, por ejemplo en 2D podemos hacer infinitos polígonos regulares (lados iguales) pero en 3D los poliedros regulares (caras iguales) que se pueden fabricar solo son 5, los sólidos platónicos (tetraedro, cubo, octaedro, dodecaedro e icosaedro).

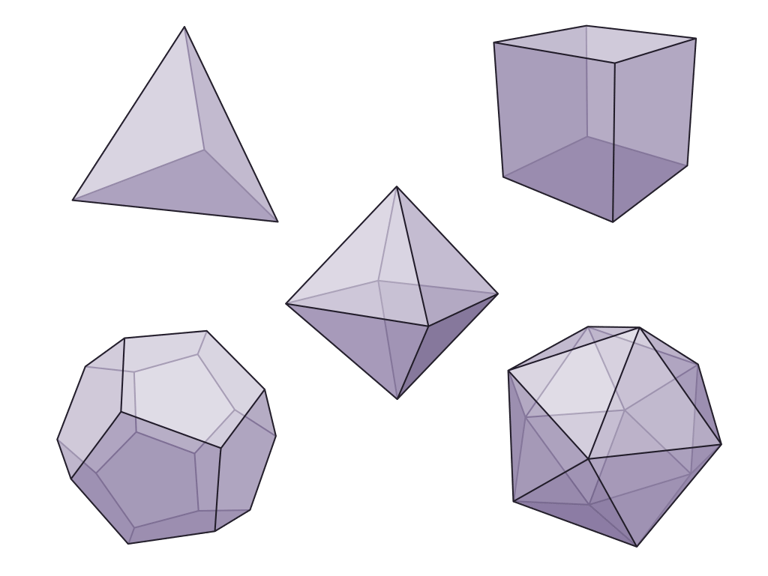
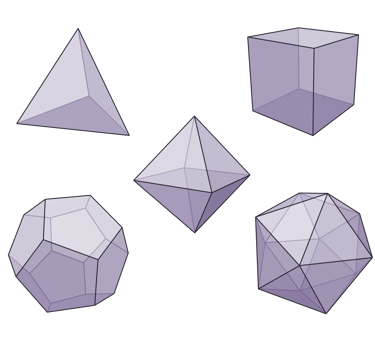
Sólidos platónicos, los únicos poliedros regulares que existen en 3 dimensiones (Fuente: Wikipedia)

Desde la época victoriana, las vidas en menos o más dimensiones siempre han suscitado una gran curiosidad entre las personas, como fielmente atestigua el éxito del libro “Planilandia, una novela de muchas dimensiones” escrita por Edwin Abbot en 1884, o el famoso médium (condenado por fraude en 1877) Henry Slade, que afirmaba ser capaz de transportar objetos desde la 4 dimensión. Para poder evaluar esa supuesta capacidad le solicitaron que realizara alguno de los siguientes actos: ensartar dos anillos sin romperlos, hacer un nudo en un lazo de cuerda cerrados sin cortar la cuerda, o vaciar una botella de agua sellada sin abrirla. Al igual que en el ejemplo inicial de sacar la pelota de la cuerda, estas actividades son imposibles a no ser que tengas acceso a la cuarta dimensión, para pasar los objetos a esas dimensiones. Lógicamente, Slade no fue capaz de realizar ninguno de los actos por lo que fue condenado por fraude. Otro famoso personaje que trató el tema de la cuarta dimensión, pero no de una forma fraudulenta, fue Charles Hinton, matemático que afirmó que en un papel, las representaciones de objetos en 3D eran siempre bidimensionales (aplanadas en la página), por ello, deberíamos ser capaces de predecir qué forma tridimensional tendría un objeto tetradimensional. De esta forma, se fueron deduciendo figuras como la del hipercubo entre otras (aparece en la imagen principal del artículo). Esto tuvo enorme influencia en el arte contemporáneo de la época, en donde artistas como Duchamp, Picasso o Dalí entre otros, realizaron diversas obras en las que reflexionaban y trataban de plasmar esas dimensiones superiores a través de sus trazos. Por lo tanto, podemos concluir que este ignoto campo de investigación se apoya simultáneamente en los avances científicos de los pensadores más brillantes, como en las obras de los más talentosos artistas.

Artículo basado en: