Un jaque mate a los terraplanistas con más de 2.000 años de antigüedad

A día de hoy, gracias a las enormes redes de difusión que representan los medios digitales, las conspiraciones y los movimientos anti-intelectuales proliferan como champiñones. Es muy posible que conozcas varias de estas conspiraciones, pero una de las que más “adeptos” o “seguidores” ha logrado es la conspiración terraplanista. Aunque parezca ilógico que en pleno siglo XXI creencias acientíficas como esta puedan penetrar en el imaginario colectivo, lo cierto es que lo hacen. Esto puede suponer un gran problema cuando estas corrientes se inmiscuyen en la salud pública, como el caso de las antivacunas (consultar artículo). Por ello, con la intención de arrojar luz sobre la oscuridad conspiratoria, en este artículo veremos cómo un astrónomo griego que vivió hace más de 2.000 años pudo determinar con gran precisión la circunferencia de la Tierra y, por lo tanto, demostrar que era esférica (más bien ovalada). Su nombre: Eratóstenes.

Hoy en día, sabemos con certeza (por mucho que les cueste creer a los ingenuos) que la Tierra no es completamente esférica, sino que está ligeramente achatada por los polos. Mientras que la longitud del meridiano que atraviesa los dos polos terrestres es de 39.942 km, la circunferencia ecuatorial (longitud del ecuador) es de 40.074 km. Cómo podemos ver, se trata de un achatamiento muy leve, apenas un 0,33%. Estos datos no son algo novedoso, ya que la primera medida del meridiano data del año 235 a.C. y la llevó a cabo Eratóstenes de Cirene, uno de los directores más ilustres de la Biblioteca de Alejandría.

Eratóstenes nació en Cirene (actual Libia), en el año 273 a.C., en una familia rica gracias a lo cual recibió una educación fantástica en Atenas y Alejandría. Durante su vida se hizo amigo de Arquímedes y ambos se profesaban un gran respeto mutuo. A lo largo de su educación, cultivó las matemáticas, la poesía, la astronomía, la geografía o la filosofía, por lo que muchos le llamaban “beta”, ya que su destino era estar detrás del alfa, es decir, aprendiz de todo pero maestro de nada. En la época en la que vivió, existía un hecho conocido por mucha gente, y es que en una ciudad llamada Siena (actual Asuán en Egipto) un cierto día del año (el solsticio de verano) al mediodía, los obeliscos y las columnas de la ciudad no arrojaban sombra. Es más, el fondo de los pozos era perfectamente visible y reflejaba como un espejo la luz del sol. Hoy en día podemos interpretar este hecho como que los rayos sol en ese día y a esa hora, apuntaban directamente al centro de la Tierra. Asuán, está situada a 24º Norte del Ecuador, y teniendo en cuenta los 23,5º de inclinación del eje terrestre, hace que en el solsticio de verano los rayos del sol incidan de forma perpendicular a la Tierra, desarrollando los fenómenos mencionados (la diferencia de 0,5º es apenas perceptible). Como Eratóstenes era también geógrafo, poseía varios de los mejores mapas de aquel entonces. Por lo que dedujo que la ciudad en la que vivía (Alejandría) estaba situada en el mismo meridiano que Asuán, lo cual era ligeramente incorrecto, pero bastante aproximado. Suponiendo que el sol está tan lejos como para que todos sus rayos inciden de forma paralela a la Tierra, se podría calcular el tamaño de ésta, simplemente midiendo la sombra que producía una columna en Alejandría, y midiendo la distancia que separaba ambas ciudades (Alejandría-Asuán).

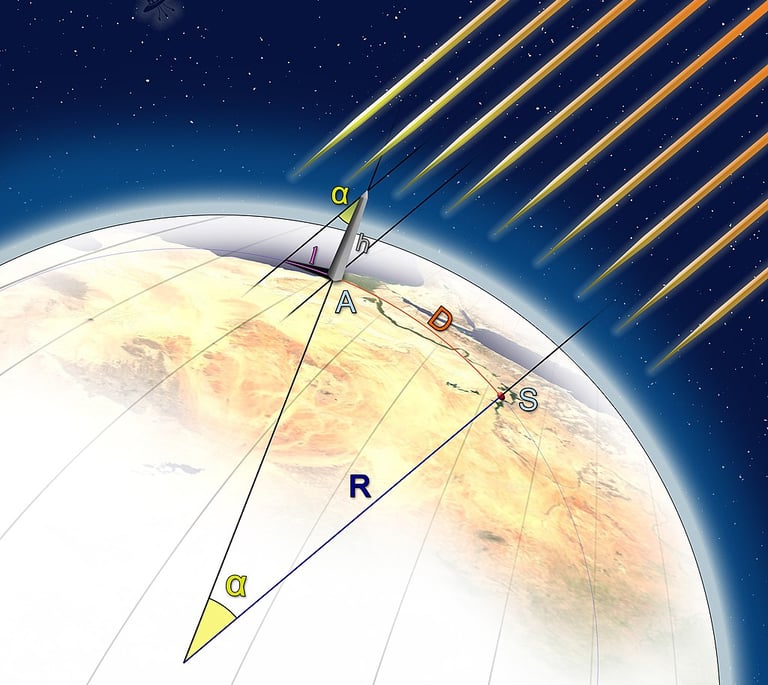
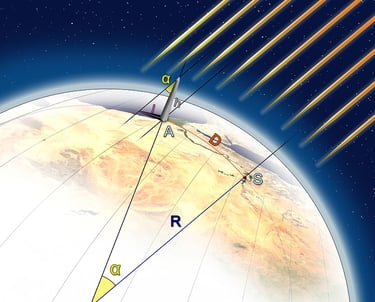
Cálculo realizado por Eratóstenes. A: Alejandría S: Asuán (Fuete: Francesco De Lorenzo)

En aquella época, las modernas técnicas de medición de distancias eran inexistentes, por lo que ¿cómo demonios iba a averiguar la distancia exacta entre ambas ciudades? Los mapas no eran tan precisos como para proporcionar una distancia exacta, entonces se le ocurrió una idea, usaría las caravanas. En el año siguiente, los jefes de todas las caravanas que viajaban a la vera del Nilo tuvieron una extraña tarea financiada por el ilustre director de la Biblioteca de Alejandría: debían medir la distancia entre las dos ciudades. Para ello tuvieron que poner a varios esclavos a contar las vueltas que daban las ruedas de los carromatos, a extender largas cuerdas a lo largo del camino o a contar pasos. Una tarea muy laboriosa teniendo en cuenta que la distancia era de más de 700 km. Cuando se acercaba el verano, mediante la información proporcionada por los jefes de las caravanas, Eratóstenes dio por buena la distancia de 5.000 estadios. Cuando llegó el día del solsticio, el impaciente astrónomo midió el ángulo que marcaba la sombra de un palo colocado perfectamente en vertical. Concluyó que era la cincuentava parte de una circunferencia completa, es decir unos 7,2º (360º / 50 = 7,2º). Por lo tanto, la Tierra tenía que estar en la misma proporción respecto a la distancia entre Asuán y Alejandría: 50 veces 5.000 estadios, 250.000 estadios. Como se observa en la imagen, el ángulo que separaba las dos ciudades (desde el centro de la Tierra), es el mismo que el de la sombra arrojada por el palo, por lo tanto, con una sencilla regla de 3, si conocemos la distancia entre ambas ciudades y el ángulo que las separa (7,2º), podremos hallar la distancia de la circunferencia de la Tierra (360º).

Según la “Historia natural” de Plinio, un estadio equivale a 1/40 schinos egipcios, un schoino representa 12.000 covados reales egipcios, y en los museos actuales se puede verificar que un covado real egipcio equivale a 0.525 metros. Es decir, un estadio equivale a 157,5 metros, lo que hace que la circunferencia de la Tierra medida por Eratóstenes sea de 39.375 km, que si la comparamos con los datos actuales (39.942 km) solo muestra un error del 1,5%, algo sorprendente teniendo en cuenta que estos cálculos se realizaron hace 2.200 años. Aun así, este error es comprensible ya que la distancia entre ambas ciudades estaba mal calculada (4.628 estadios en vez de 5.000) y Alejandría y Asuán no se encuentran en el mismo meridiano, sino que existe una diferencia de unos 3º de longitud. No obstante, su labor de medición fue algo impresionante. Este mismo cálculo puedes hacer tú mismo si tienes la suerte de tener un amigo o familiar en una ciudad situada a varios cientos de kilómetros, que se encuentre en el mismo meridiano que la tuya, lo cual puede servir para aclarar las dudas de los más escépticos terraplanistas, ya que como dijo Confucio: “Me lo contaron y lo olvidé. Lo vi y lo creí. Lo hice y lo aprendí”.

Artículo basado en: